UNIDAD (1) CLASE (3) INTEGRALES Y CAMBIO DE VARIABLES

INTEGRALES Y CAMBIO DE VARIABLE

1.- El dia sabado ( primero de Junio ) nos toco un nuevo tema sobre integrales y cambio de variable la verdad no comprendi muy bien este tema me quedaron dudas ya que andaba enfermo y no me pude consentrar, profe espero entenderle un poco mejor este cuatrimestre me ira mejor que el pasado .

2.- INTEGRACION POR CAMBIO DE VARIABLE

Como indica su nombre, este método de integración consiste en la aplicación de un cambio de variable para simplificar el integrando. No vamos a explicar el método formalmente, pero los pasos a seguir son los siguientes:

Método de integración por sustitución:

Escoger un cambio de variable $z =$ función de $x$ .
Despejar $x$ para calcular $d x$ .
Sustituir en la integral y resolverla.
Deshacer el cambio de variable.

Ejemplo

Vamos a resolver una integral muy sencilla (es una integral directa) por el método de sustitución. Consideremos la siguiente integral:

Resolución detallada de integrales mediante el método de integración por sustitución o cambio de variable. Integrales resueltas y explicadas. Bachiller, bachillerato, universidad, cálculo integral.

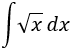
1. Buscamos un cambio de variable que sea función de $x$ , por ejemplo,

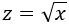
2. Aislamos $x$ y derivamos:

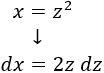
3. Sustituimos en la integral:

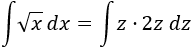
Observad que hemos cambiado $\sqrt{x}$ por $z$ y $d x$ por $2 z d z$ . Resolvemos la integral:

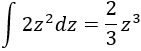
4. Ya sólo queda deshacer el cambio de variable:

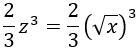
Por tanto, la integral inicial es

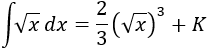
Nota: no olvidemos la constante de integración (a la que hemos llamado $K$ ).

La dificultad del método es escoger un cambio útil, ya que, en caso contrario, la integral resultante puede ser de mayor dificultad. En la siguiente tabla se recogen los cambios de variable que tienen alta probabilidad de funcionar en las integrales que usualmente veremos:

El método de cambio de variable es un poco más complicado cuando se aplica en integrales definidas porque, al cambiar la variable, deben actualizarse los extremos de integración. Por ejemplo, si los extremos de la integral inicial con variable $x$ son 0 y 1 y la nueva variable es $z = 2 x$ , entonces, los nuevos extremos serán 0 y 2. No obstante, una sencilla forma de evitar este problema es resolver primero la integral indefinida.

Los pasos para resolver una integral mediante el método de integración por sustitución o cambio de variable son:

Escogemos la expresión algebraica de la integral que queremos sustituir y cual será el cambio de variable.
$u=g(x)$
Derivamos en los dos lados de la ecuación para calcular dx.
$du=g'(x)dx$
Hacemos el cambio de variable en la integral. Para ello, debemos sustituir la expresión algebraica que hemos escogido por u y, además, sustituir dx por la expresión calculada en el paso anterior.
$\displaystyle\int f(u)\ du$
Resolvemos la integral obtenida.
Deshacemos el cambio de variable para obtener el resultado de la integral original.
$u \ \color{orange}\bm{\longrightarrow}\color{black}\ g(x)$

$\displaystyle \int u^4 \ du$

De este modo podemos resolver fácilmente la integral aplicando la fórmula de las integrales de potencias:

$\displaystyle \int u^4 \ du=\frac{u^5}{5}+C$

Una vez hemos resuelto la integral, deshacemos el cambio de variable para hallar el resultado de la integral original:

$\displaystyle \frac{u^5}{5}+C=\frac{\text{sen}^5(x)}{5}+C$

Y de esta forma hemos conseguido solucionar la integral mediante el método de sustitución. Como puedes ver, este método de integración permite resolver integrales complicadas de manera más fácil. A continuación te dejamos varios ejercicios resueltos del método de integración por sustitución para que puedas practicar.

Resuelve la siguiente integral logarítmica por el método de sustitución:

$\displaystyle\int\frac{1}{x\sqrt{1-\ln(x)}} \ dx$

EL SESULTADO SERIA:

El cambio de variable que tenemos que hacer en esta integral para resolverla es el siguiente:

$u=1-\ln(x)$

$\displaystyle du=-\frac{1}{x}\ dx$

De modo que al hacer el cambio de variable la integral queda de la siguiente manera:

$\displaystyle\int\frac{1}{x\sqrt{1-\ln(x)}}\ dx= \int -\frac{1}{\sqrt{u}}\ du$

Resolvemos la integral de la raíz convirtiéndola primero a una potencia:

$\displaystyle\int -\frac{1}{\sqrt{u}}\ du=-\int u^{-1/2}\ du = -\frac{u^{1/2}}{\frac{1}{2}}\ du = -2\sqrt{u}+C$

Y, por último, deshacemos el cambio de variable:

$\displaystyle -2\sqrt{u}+C=-2\sqrt{1-\ln(x)}+C$

SEGUNDO EJERCICIO:

Resuelve la siguiente integral de un cociente de funciones exponenciales:

$\displaystyle\int\frac{5^{2x}}{1+5^{2x}} \ dx$

El cambio de variable a aplicar para calcular la integral es:

$u=5^{2x}$

$\displaystyle du=2\ln(5)\cdot 5^{2x}\ dx \ \longrightarrow \ 5^{2x} \ dx=\frac{du}{2\ln(5)}$

La integral con el cambio de variable hecho es:

$\displaystyle\int\frac{5^{2x}}{1+5^{2x}} \ dx=\int\frac{1}{1+u}\cdot \frac{du}{2\ln(5)} = \frac{1}{2\ln(5)}\int\frac{1}{1+u}\ du$

La integral obtenida es bastante más fácil de resolver, pues es logarítmica:

$\displaystyle\frac{1}{2\ln(5)}\int\frac{1}{1+u}\ du=\frac{1}{2\ln(5)}\cdot \ln(1+u)+C$

Finalmente, solo nos queda deshacer el cambio de variable para determinar la solución:

$\displaystyle \frac{1}{2\ln(5)}\cdot \ln(1+u)+C=\frac{\ln\left(1+5^{2x}\right)}{2\ln(5)}+C$

3.- IMAGENES

4.- VIDEOS

5.- LINKS DE DONDE SE ENCUENTRA LA INFORMACION

▷ Integración por sustitución (o cambio de variable) (funciones.xyz)

Método de integración por cambio de variable o sustitución: integrales resueltas (matesfacil.com)

Kevin Eduardo López machorro

Buscar este blog